Vlastnosti jednotných buniek, červená konštanta a typy

Ten Jednotka Je to imaginárny priestor alebo oblasť, ktorá predstavuje minimálne vyjadrenie celku; Že v prípade chémie by bol celok kryštálom zložený z atómov, iónov alebo molekúl, ktoré sú usporiadané podľa štrukturálneho vzoru.

V každodennom živote nájdete príklady, ktoré stelesňujú tento koncept. Z tohto dôvodu je potrebné venovať pozornosť objektom alebo povrchom, ktoré vykazujú určité opakujúce sa poradie svojich prvkov. Niektoré mozaiky, bas -relief, remeslo.

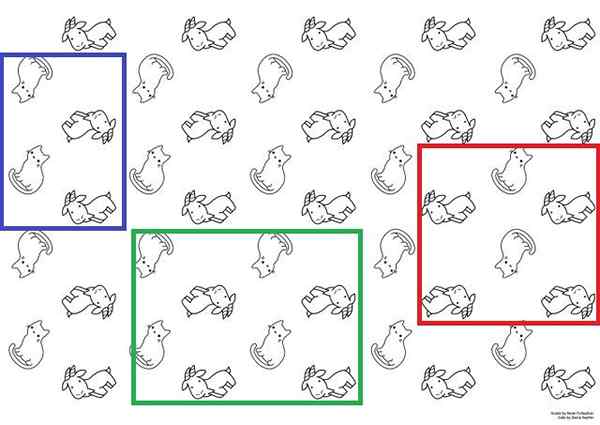Unitárne bunky na papieri pre mačky a kozie. Zdroj: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // creativeCommons.Org/licencie/By-SA/4.0)].

Na jasnejšie ilustráciu máte vynikajúci obraz, ktorý by sa mohol použiť ako tapisériový papier. V ňom sa objavujú mačky a kozy s dvoma alternatívnymi zmyslami; Mačky sú nohy alebo hlava a kozy sa pozerajú hore alebo dole.

Tieto mačky a kozy vytvárajú opakujúcu sa štrukturálnu sekvenciu. Na vybudovanie všetkého papiera by stačilo na reprodukciu jednotnej bunky na povrch.

Možné jednotkové bunky sú znázornené modrou, zelenou a červenou škatuľou. Ktorýkoľvek z týchto troch by sa mohol použiť na získanie papiera; Je však potrebné ich predstaviť imagne po povrchu, aby ste zistili, či reprodukujú rovnakú sekvenciu pozorovanú na obrázku.

Počnúc červenou skrinkou by sa ocenilo, že ak by sa tri stĺpce (mačiek a kôz) presunuli doľava, v dolnej časti by sa už neobjavili dve kozy, ale iba jedna, ale iba jedna. Preto by to viedlo k inej sekvencii a nemožno ho považovať za jednotkovú bunku.

Zatiaľ čo ak si predstavujú, že posúvajú dve škatule, modré a zelené, získa sa rovnaká sekvencia papiera. Obidve sú jednotkové bunky; Blue Box však definíciu viac dodržiava, pretože je menšia ako zelená skrinka.

[TOC]

Vlastnosti jednotkových buniek

Jeho vlastná definícia, okrem novo vysvetleného príkladu, objasňuje aj niekoľko jeho vlastností:

-Ak sa pohybujú vo vesmíre, bez ohľadu na smer, získa sa úplná pevná látka alebo sklo. Je to preto, že, ako sa uvádza v prípade mačiek a kôz, reprodukujú štrukturálnu sekvenciu; čo sa rovná priestorovému rozloženiu opakujúcich sa jednotiek.

-Musia byť čo najmenší (alebo zaberať malý objem) v porovnaní s inými možnými možnosťami buniek.

Môže vám slúžiť: kyselina metylmalónová: štruktúra, vlastnosti, syntéza, použitie

-Sú obyčajné, symetrické. Podobne sa jej symetria doslova odráža v kryštáloch zlúčeniny; Ak je jednotková bunka soli kubická, jej kryštály budú kubické. Existujú však kryštalické štruktúry opísané s jednotkovými bunkami so skreslenými geometriami.

-Obsahujú opakujúce sa jednotky, ktoré môžu byť nahradené bodmi, ktoré na druhej strane -rozmerne to, čo sa nazýva sietnicami. V predchádzajúcom príklade mačky a kozy predstavujú retikulárne body pozorované z vyššej roviny; to znamená, dve rozmery.

Počet opakujúcich sa jednotiek

Opakované jednotky alebo sietnice jednotkových buniek udržiavajú rovnaký podiel tuhých častíc.

Ak sa počet mačiek a kôz vo vnútri modrej škatule, budú dve mačky a kozy. To isté platí pre zelenú škatuľu a tiež s červenou škatuľou (aj keď je už známe, že nejde o jednotkovú bunku).

Predpokladajme napríklad, že mačky a kozy sú atómy G a C, respektíve podivné zviera zvárania). Pretože pomer medzi G a C je 2: 2 alebo 1: 1 v modrej škatuli, dá sa bez chýb očakávať, že pevná látka bude mať vzorec GC (alebo CG).

Ak má tuhá látka viac alebo menej kompaktné štruktúry, ako v prípade soli, kovov, oxidov, sulfidov a zliatiny, v jednotkových bunkách neexistujú žiadne celé opakujúce sa jednotky; to znamená, že existujú časti alebo časti, ktoré zvyšujú jednu alebo dve jednotky.

To nie je prípad GC. Ak by modrá box „začala“ pre mačky a kozy v dvoch (1/2G a 1/2C) alebo štyri časti (1/4G a 1/4C). V nasledujúcich častiach bude zrejmé, že v týchto jednotkových bunkách sú retikulárne body vhodne rozdelené týmto a inými spôsobmi.

Aké sieťové konštanty definujú jednotkovú bunku?

Unitárne bunky príkladu GC sú dve rozmerové; To sa však neuplatňuje v skutočných modeloch, ktoré zvažujú tri rozmery. Škatule alebo rovnobežky sa tak transformujú na paralellepípedos. Termín „bunka“ má teraz väčší zmysel.

Rozmery týchto buniek alebo paralelnepipedov závisia od toho, ako dlho sú ich príslušné strany a uhly.

Na dolnom obrázku máte dolný zadný roh paralepiped, ktorý sa skladá zo strán do, b a c, a uhly a, p a y.

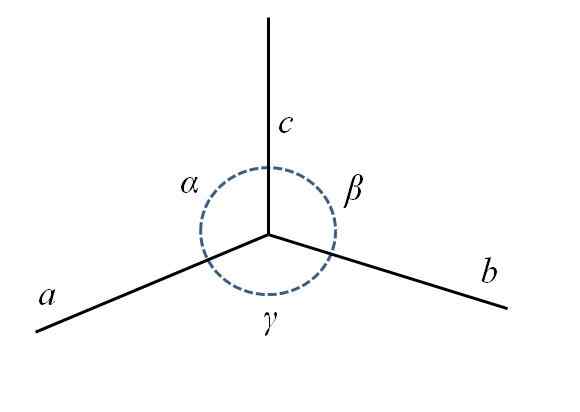Parametre jednotkovej bunky. Zdroj: Gabriel Bolívar.

Ako môžeš vidieť, do je o niečo dlhšie ako b a c. V strede máte kruh s bodkovanou čiarou na označenie uhlov a, β a y, Ac, Cb a BA, respektíve. Pre každú jednotkovú bunku majú tieto parametre konštantné hodnoty a definujú ich symetriu a zvyšok skla.

Môže vám slúžiť: peroxid vápenatý (CAO2): vlastnosti, riziká a použitia

Parametre obrazu by znova použili určitú fantáziu, definovali by bunku podobnú roztiahnutej kocke na jej okraji do. Jednotkové bunky teda vznikajú s rôznymi dĺžkami a uhlami jej okrajov, ktoré možno tiež klasifikovať do rôznych typov.

Chlapci

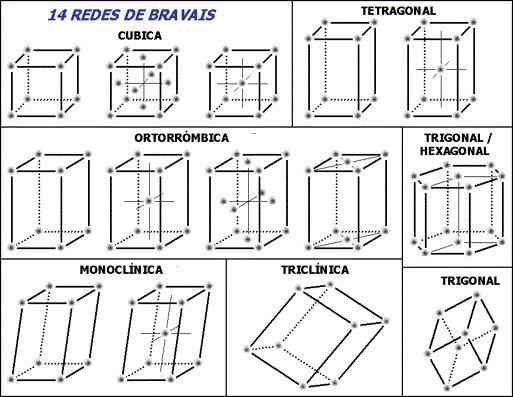
14 sietí Bravais a sedem základných kryštalických systémov. Zdroj: Pôvodný Uploader bol Angrense v Portugalskej Wikipédii. [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Poznámka, aby ste spustili bodkované čiary vo vnútri jednotkových buniek: označujú spodný zadný uhol, ako je vysvetlené. Je možné položiť nasledujúcu otázku, kde sú retikulárne body alebo opakujúce sa jednotky? Aj keď vyvolávajú nesprávny dojem, že bunky sú prázdne, vo svojich vrcholoch odpoveď leží.

Tieto bunky sa generujú alebo vyberajú takým spôsobom, že vo svojich vrcholoch sú opakujúce sa jednotky umiestnené (sivé body obrázka). V závislosti od hodnôt parametrov stanovených v predchádzajúcej časti je odvodených konštanta pre každú jednotkovú bunku, sedem kryštalických systémov.

Každý kryštalický systém má svoju vlastnú jednotnú bunku; Druhý definuje prvý. Na hornom obrázku je sedem políčok, ktoré zodpovedajú siedmim kryštalickým systémom; Alebo trochu viac súhrnných kryštalických sietí. Napríklad bunka kubickej jednotky zodpovedá jednému z kryštalických systémov, ktorý definuje kubickú kryštalickú sieť.

Podľa obrázka sú kryštalické systémy alebo siete:

-Kubický

-Tetragonálny

-Ortorrombika

-Šesťuholníkový

-Monoklinický

-Triklinický

-Trigonálny

Av týchto kryštalických systémoch ostatné, ktoré tvoria štrnásť sietí Bravais; že medzi všetkými kryštalickými sieťami sú najzákladnejšie.

Kubický

V kocke sú všetky jej strany a uhly rovnaké. V tejto jednotkovej bunke sa preto splní nasledujúce:

do = b = c

a = p = γ = 90 °

Existujú tri bunky kubickej jednotky: jednoduché alebo primitívne, sústredené na telo (BCC) a sústredené na tváre (FCC). Rozdiely spočívajú v tom, ako sa distribuujú body (atómy, ióny alebo molekuly) a v počte z nich.

Ktorá z týchto buniek je najkompaktnejšia? Že ktorého objem je viac obsadený bodmi: kubický sústredený na tváre. Všimnite si, že ak nahradíme body za mačky a kozy začiatku, neboli by obmedzené na jednu bunku; Patrili by a mali by byť zdieľaní niekoľkými. Opäť by to boli porcie g alebo c.

Môže vám slúžiť: hydrokoloid

Počet jednotiek

Keby boli mačky alebo kozy vo vrcholoch, boli by zdieľané 8 jednotkovými bunkami; To znamená, že každá bunka by mala 1/8 G alebo C. Spoločne alebo si predstavte 8 kociek, v dvoch stĺpcoch po dvoch riadkoch, aby ste si to vizualizovali.

Keby boli mačky alebo kozy na tvári, zdieľali by ich iba 2 jednotkové bunky. Aby som to videl, stačí zhromaždiť dve kocky.

Na druhej strane, ak by mačka alebo koza boli v strede kocky, patrili by iba do jednej jednotnej bunky; To isté sa deje s políčkami hlavného obrázka, keď bol koncept riešený.

Povedal potom vyššie uvedené, v jednoduchej kubickej bunke a Jednotkový alebo retikulárny bod, pretože má 8 vrcholov (1/8 x 8 = 1). Pre kubickú bunku vycentrovanú v tele, ktoré máte: 8 vrcholov, ktoré sa rovnajú atómu a bodom alebo jednotkou v strede; Preto existuje dva Jednotky.

A pre kubickú bunku zameranú na tváre, ktoré máte: 8 vrcholov (1) a šesť tvárí, v ktorých sa zdieľajú polovica každého bodu alebo jednotky (1/2 x 6 = 3); Preto má štvorka Jednotky.

Tetragonálny

Podobné komentáre sa dajú urobiť s ohľadom na jednotnú bunku pre tetragonálny systém. Jeho štrukturálne parametre sú nasledujúce:

do = b ≠ c

a = p = γ = 90 °

Ortorrombika

Parametre pre otorrombickú bunku sú:

do ≠ b ≠ c

a = p = γ = 90 °

Monoklinický

Parametre pre monoklinickú bunku sú:

do ≠ b ≠ c

a = γ = 90 °; β ≠ 90 °

Triklinický

Parametre pre triclinickú bunku sú:

do ≠ b ≠ c

α ≠ β ≠ γ ≠ 90 °

Šesťuholníkový

Parametre pre šesťuholníkovú bunku sú:

do = b ≠ c

a = β = 90 °; γ ≠ 120 °

V skutočnosti bunka predstavuje tretiu časť hexagonálneho hranolu.

Trigonálny

A nakoniec, parametre pre trigonálnu bunku sú:

do = b = c

α = β = γ ≠ 90 °

Odkazy

1. Whitten, Davis, Peck & Stanley. (2008). Chémia. (8. vydanie.). Cengage Learning P 474-477.
2. Triasť a Atkins. (2008). Anorganická chémia. (Štvrté vydanie). MC Graw Hill.
3. Wikipedia. (2019). Primitívna bunka. Zdroj: In.Wikipedia.orgán
4. Bryan Stephanie. (2019). Jednotková bunka: parametre latice a kubické štruktúry. Štúdium. Získané z: štúdie.com
5. Centrum akademických zdrojov. (s.F.). Krištáľové štruktúry. [PDF]. Technologický inštitút Illinois. Zdroj: Web.iIT.Edu
6. Belford Robert. (7. februára 2019). Krištáľové latices a jednotkové bunky. Chémia librettexts. Získané z: Chem.Librettexts.orgán