Axiálne zaťaženie Ako vypočítané a vyriešené cvičenia

Ten Axiálne zaťaženie Je to sila, ktorá je nasmerovaná paralelne s osou symetrie prvku, ktorá tvorí štruktúru. Axiálna sila alebo zaťaženie môže byť napätie alebo kompresia. Ak sa línia pôsobenia axiálnej sily zhoduje s osou symetrie, ktorá prechádza cez zvažovanú strednú časť prvku, potom sa hovorí, že ide o sústredné axiálne zaťaženie alebo silu.

Naopak, ak ide o axiálnu silu alebo zaťaženie rovnobežnú so osou symetrie, ale ktorej línia pôsobenia nie je na samotnej osi, je to excentrická axiálna sila.

postava 1. Axiálne zaťaženie. Zdroj: Self Made

Na obrázku 1 žlté šípky predstavujú sily alebo axiálne zaťaženie. V jednom prípade je to koncentrická napätá sila a v druhom čelíme excentrickej kompresnej sile.

Jednotka miery axiálneho zaťaženia v medzinárodnom systéme, ak je to Newton (n). Ale často sa používajú iné silové jednotky, ako je kilogramová sila (kg-f) a sila libry (LB-F) (LB-F).

[TOC]

Ako sa vypočítava?

Na výpočet hodnoty axiálneho zaťaženia v prvkoch štruktúry sa musia dodržiavať nasledujúce kroky:

- Vytvorte si silovú schému na každom prvku.

- Aplikujte rovnice, ktoré zaručujú translačný zostatok, to znamená, že súčet všetkých síl je neplatný.

- Zvážte rovnicu krútiacich momentov alebo momentov, aby sa splnila rotačná rovnováha. V tomto prípade musí byť suma všetkých krúžkov null.

- Vypočítajte sily, ako aj identifikujte axiálne sily alebo zaťaženia v každom z prvkov.

Vzťah axiálneho zaťaženia s normálnym úsilím

Priemerné normálne úsilie je definované ako kvocient medzi axiálnym zaťažením rozdeleným medzi prierez oblasti. Jednotky normálneho úsilia v medzinárodnom systéme S.Jo. Sú to Newton na štvorcových metroch (N/ m²) alebo Pascal (PA). Obrázok 2 zobrazuje koncept normálneho úsilia pre prehľadnosť.

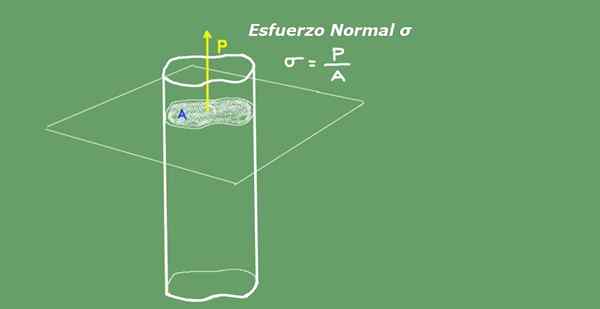Obrázok 2. Normálne úsilie. Zdroj: Self Made.

Vyriešené cvičenia

-Cvičenie 1

Zvážte valcový betónový stĺpec H a rádio R. Predpokladajme, že hustota betónu je ρ. Stĺpec nepodporuje žiadne ďalšie zaťaženie ako jeho vlastná hmotnosť a je podopretý na obdĺžnikovej základni.

- Nájdite hodnotu axiálneho zaťaženia v bodoch A, B, C a D, ktoré sú v nasledujúcich pozíciách: a na spodnej časti stĺpca, b a ⅓ výšky h, c a ⅔ výšky H a posledným d na hornom konci stĺpca.

- Určte tiež priemerné normálne úsilie v každej z týchto pozícií. Zoberme si nasledujúce numerické hodnoty: h = 3m, r = 20 cm a ρ = 2250 kg/m³

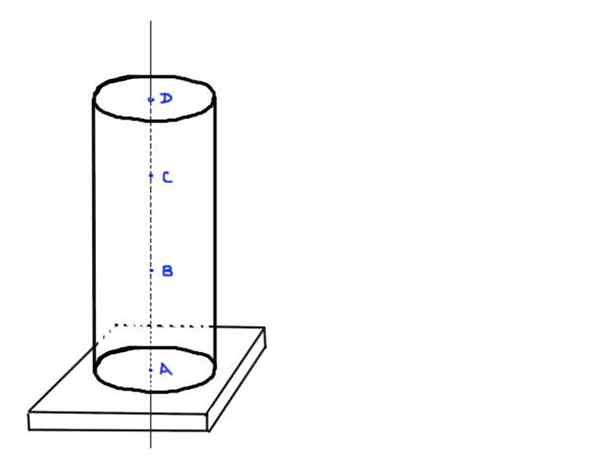Obrázok 3. Valcový. Zdroj: Self Made.

Riešenie

Celková hmotnosť stĺpca

Celková hmotnosť W v stĺpci je produktom jeho hustoty objemom vynásobeným zrýchlením gravitácie:

W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 n

Axiálne zaťaženie v a

V bode do stĺpca musí podporovať celú svoju váhu, aby sa axiálne zaťaženie v tomto bode stalo kompresiou, ktorá sa rovná hmotnosti stĺpca:

Pa = w = 8313 n

Axiálne zaťaženie v B

V bode B bude sám ⅔ zo stĺpca, takže axiálne zaťaženie v tomto bode bude kompresia a jeho hodnota hmotnosti stĺpca:

Pb = ⅔ w = 5542 n

Obrázok 3. Valcový. Zdroj: Self Made.

Nad polohou C Existuje iba stĺpec ⅓, takže jeho axiálne kompresné zaťaženie bude ⅓ vlastnej hmotnosti:

PC = ⅓ w = 2771 n

Axiálne zaťaženie v D

Nakoniec v bode D, to je horný koniec stĺpca, nie je zaťaženie, takže axiálna sila v tomto bode je prázdna.

PD = 0 n

Normálne úsilie v každej z pozícií

Na určenie normálneho úsilia v každej z pozícií bude potrebné vypočítať prierez oblasti A, ktorý je daný:

A = π ∙ R² = 0,126 m²

Týmto spôsobom bude normálnym úsilím v každej z pozícií kvocientom medzi axiálnou silou v každom z bodov rozdelených medzi už vypočítaný prierez, ktorý je v tomto cvičení rovnaký pre všetky body, pretože ide.

σ = p/a; σa = 66,15 kPa; σb = 44,10 kPa; σc = 22,05 kPa; σd = 0,00 kPa

-Cvičenie 2

Obrázok ukazuje štruktúru zloženú z dvoch barov, ktoré zavoláme AB a CB. AB Bar je na konci podporovaný a po druhom cez kolík a na druhom konci pripojený k druhej liške cez inú b -pin.

Podobne je CB lišta podopretá na konci C pomocou špendlíka a na konci B s kolíkom B, ktorý ho spája na druhú tyč. Na kolíky B sa aplikuje vertikálna sila alebo zaťaženie F, ako je znázornené na nasledujúcom obrázku, ukazuje:

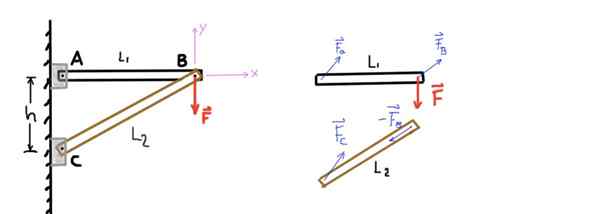Obrázok 4. Štruktúra dvoch tyčí a diagram voľného tela. Zdroj: Self Made.

Predpokladajme, že hmotnosť tyčí sa opovrhuje, pretože sila f = 500 kg-f je oveľa väčšia ako hmotnosť štruktúry. Oddelenie podpory A a C je H = 1,5 m a dĺžka AB lišty je L1 = 2 m. Stanovte axiálne zaťaženie v každej zo stĺp.

Riešenie 2

Obrázok ukazuje, prostredníctvom diagramu voľného tela, sily pôsobiace na každý z prvkov štruktúry. Je tiež uvedený karteziánsky súradnicový systém, s ktorým sa zvýšia rovnovážné rovnice síl.

Krútiace momenty alebo momenty sa vypočítajú v bode B a budú sa považovať za pozitívne, ak poukazujú z obrazovky (os z). Rovnováha síl a krútiacich momentov pre každý stĺpec je:

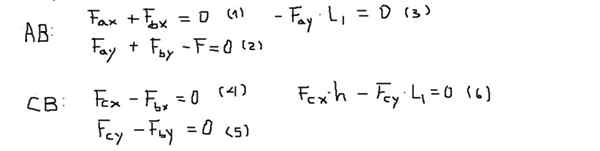
Potom sú zložky síl každej z rovníc jasné po nasledujúcom poradí:

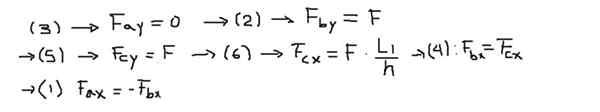
Nakoniec sa výsledné sily počítajú na koncoch každej tyče:

Dá sa poznamenať, že sily na koncoch každej z tyčí sú s nimi rovnobežné a potvrdzujú, že ide o axiálne sily alebo zaťaženia. V prípade tyče AB je to axiálne napätie, ktorej hodnota je:

F ∙ (L1/H) = 500 kg-f ∙ (2,0 m/1,5 m) = 666,6 kg-f = 6533,3 n

CB bar je v kompresii kvôli dvom silám, ktoré pôsobia na ich koncoch, ktoré sú paralelné s barom a ukazujú na svoje stred. Veľkosť axiálnej kompresnej sily v lištách CB je:

F ∙ (1 + l12/h²) 1/2 = 500 kg-f ∙ (1 + (2/1,5) ²) 1/2 = 833,3 kg-f = 8166,6 n

Odkazy

1. Pivo f ... mechanika materiálu. 5. Vydanie. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Mechanika materiálov. Ôsme vydanie. Sála. 2011. 3-60.
3. Gere J. Mechanika materiálov. Ôsme vydanie. Učenie sa. 4-220.
4. Giancoli, D. 2006. Fyzika: Princípy s aplikáciami. 6. vydanie. Sála. 238-242.
5. Valera Negrete, J. 2005. Všeobecné fyzikálne poznámky. Žobrák. 87-98.