Koncepty, metódy, príklady, príklady

On Analýza Je to technika používaná na riešenie plochých elektrických obvodov. Tento postup sa môže objaviť aj v literatúre s názvami metód obvodové prúdy o metóda Sieťové prúdy (alebo slučka).

Základ tohto a ďalšie metódy analýzy elektrických obvodov sú v zákonoch Kirchhoff a Ohmovho zákona. Kirchhoffove zákony sú zase výrazy dvoch veľmi dôležitých princípov ochrany vo fyzike pre izolované systémy: Zachovávajú sa elektrické a energia.

postava 1. Obvody sú súčasťou nespočetných zariadení. Zdroj: Pixabay.

Na jednej strane elektrický náboj súvisí so prúdom, ktorý sa pohybuje zaťaženie, zatiaľ čo v obvode je energia spojená s napätím, čo je agent zodpovedný za vykonanie potrebnej práce na udržanie zaťaženia v pohybe.

Tieto zákony, ktoré sa uplatňujú na plochý obvod, generujú súbor súčasných rovníc, ktoré sa musia vyriešiť, aby sa získali hodnoty prúdu alebo napätia.

Systém rovníc možno vyriešiť už známymi analytickými technikami, ako napríklad Pravidlo, čo vyžaduje výpočet determinantov na získanie systému systému.

V závislosti od počtu rovníc sa vyriešia pomocou vedeckej kalkulačky alebo matematického softvéru. V sieti je k dispozícii aj veľa možností.

[TOC]

Dôležité podmienky

Pred vysvetlením, ako to funguje, začneme definovaním týchto podmienok:

Pobočka: Časť obsahujúca prvok obvodu.

Uzol: Bod, ktorý spája dve alebo viac vetiev.

Stuha: Je to akákoľvek uzavretá časť obvodu, ktorá začína a končí v rovnakom uzle.

Zaviazať: slučka, ktorá neobsahuje žiadne iné zväzky vo vnútri (základná sieť).

Metódy

Semská analýza je všeobecná metóda, ktorá slúži na riešenie obvodov, ktorých prvky sú spojené v sérii, paralelne alebo zmiešanom, to znamená, keď typ spojenia nie je jasne rozlíšený. Obvod musí byť plochý, alebo musí byť aspoň možné ho splatiť ako taký.

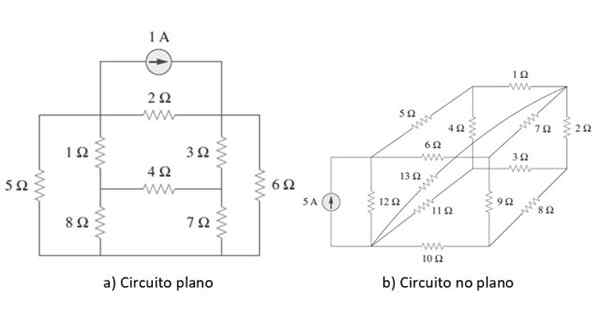Obrázok 2. Ploché a non -flat obvody. Zdroj: Alexander, C. 2006. Základy elektrických obvodov. Tretí. Vydanie. MC Graw Hill.

Príklad každého typu obvodu je uvedený na obrázku vyššie. Akonáhle je bod objasnený, začneme, uplatňujeme metódu na jednoduchý obvod ako príklad v nasledujúcej časti, ale predtým, ako stručne preskúmame zákony Ohm a Kirchhoff.

Ohmov zákon: Sean Vložka Napätie, R Odpor e Jo Prúd ohmického odporového prvku, v ktorom je napätie a prúd priamo úmerné, pričom odpor je konštantnou proporcionálnou:

Môže vám slúžiť: API Gravity: Stupnica a klasifikácia surovej

V = i.R

V napätí Kirchhoff Law (LKV): V akejkoľvek uzavretej trajektórii, ktorá sa prešla jedným smerom, je algebraický súčet napätia nula. To zahŕňa napätie v dôsledku zdrojov, odporov, induktorov alebo kondenzátorov: ∑ e = ∑ r_Jo. Jo

Kirchhoff z prúdu (LKC): V akomkoľvek uzle je algebraický súčet prúdov nula, berúc do úvahy, že prúdy, ktoré vstupujú. Týmto spôsobom: ∑ i = 0.

S metódou sieťových prúdov nie je potrebné.

- Kroky na použitie analýzy ôk

Začneme vysvetliť metódu obvodu 2 oká. Postup sa dá rozšíriť neskôr pre väčšie obvody.

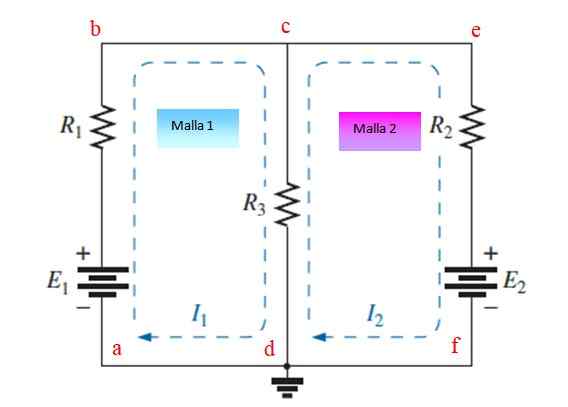Obrázok 3. Obvod s odpormi a zdrojmi usporiadanými v dvoch okách. Zdroj: f. Zapata.

Krok 1

Priraďovať a nakresliť nezávislé prúdy ku každej ôk, v tomto príklade sú Jo₁ a Jo₂. Môžu byť nakreslené v harmonograme alebo tiež anti -horlivý.

Krok 2

Aplikujte zákon o Kirchhoffovom napätí (LTK) a Ohmov zákon na každú sieť. Potenciálne pády sú priradené znamenie (-), zatiaľ čo zvýšenie je priradené znamenie (+).

ABCDA MESH

Od bodu A a po význame prúdu zistíme zvýšenie potenciálu v batérii E1 (+), potom pokles v r₁ (-) a potom ďalší spadne do r₃ (-).

Súčasne odpor R₃ Prechádza to aj súčasným i₂, Ale v opačnom smere, preto predstavuje vzostup (+). Prvá rovnica je taká:

A₁-R₁.Jo₁ -R₃.Jo₁ + R₃.Jo₂ = 0

Bezprostredne faktoring a opätovné predkladanie podmienok:

- (R₁+R₃)₁ +R₃Jo₂ = -E₁  (Rovnica 1)

Sieťovina CEFDC 

Od bodu a a dodržiavanie významu prúdu je potenciálnym poklesom v R₂ (-), ďalší spadne do A₂, Pretože prúd vstupuje cez pól batérie + a nakoniec ďalší spadne R₃ (-), súčasne aktuálny Jo₁ Prechádza to R₃ V opačnom smere (+).

Druhá rovnica, so znakmi uvedenými, zostáva týmto spôsobom:

- R₂ Jo₂ - A₂ -R₃ Jo₂ +R₃ Jo₁= 0

R₃Jo₁ - (R₂ +R₃₎ Jo₂ = E₂  (Rovnica 2)

Všimnite si, že existujú dve rovnice s dvoma neznámymi a₁ a ja₂.

Krok 3

Potom je takto vytvorený systém rovníc vyriešený.

Vyriešené cvičenia

Ak chcete začať, je dôležité vziať do úvahy nasledujúce:

-Kravaty alebo sieťové prúdy môžu byť pridelené ľubovoľný smer.

-Ku každej základnej ôk - alebo „okno“ - že obvodu musí byť priradený prúd.

Môže vám slúžiť: izotický proces

-Sieťové prúdy sa nazývajú kapitálové písmená na ich odlíšenie od prúdov, ktoré cirkulujú v pobočkách, hoci v niektorých prípadoch môže prúd, ktorý cirkuluje cez vetvu.

- Príklad 1

Nájdite prúdy, ktoré cirkulujú cez každý odpor v obvode na obrázku 3, ak prvky majú nasledujúce hodnoty:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; A₁ = 12 V; A₂ = 18 V

Riešenie

V prvom rade je potrebné priradiť prúdy siete a₁ a ja₂ a vezmite systém rovníc odvodených v predchádzajúcej časti, potom nahradte hodnoty uvedené vo vyhlásení:

- (R₁+R₃)₁ +R₃Jo₂ = -E₁  (Rovnica 1)

R₃Jo₁ - (R₂ +R₃₎ Jo₂ = E₂     (Rovnica 2)

-

-(20+30) Jo₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-päťdesiatJo₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Pretože ide o systém 2 x 2 rovníc, dá sa ľahko vyriešiť redukciou, vynásobením 5 druhou rovnicou, aby sa eliminovala neznáma Jo₁:

-päťdesiatJo₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

Jo₂ = - 78/180 A = - 0.41 a

Prúd sa okamžite vymaže Jo₁ z ktorejkoľvek z pôvodných rovníc:

Jo₁ = (18 + 40 i₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

Záporné znamenie v prúde Jo₂ znamená, že prúd v 2 ôk cirkuluje v rozpore s výkresom.

Prúdy v každom odporu sú nasledujúce:

Pre odpor R₁ Prúd cirkuluje Jo₁ = 0.16 a v tom zmysle, ktorý je nakreslený odporom R₂ Prúd cirkuluje Jo₂ = 0.41 a na rozdiel od nakreslených a pre odpor R₃ cirkulovať Jo₃ = 0.16- (-0.41) a = 0.57 a dole.

Systémové riešenie podľa Cramerovej metódy

Matrixovým spôsobom je možné systém vyriešiť takto:

Krok 1: Vypočítajte δ

 Dôležitý: Keď δ = 0, systém nemá žiadne riešenie, je to nekompatibilný systém.

Krok 2: Vypočítajte δ₁

Prvý stĺpec je nahradený nezávislými podmienkami systému rovníc, pričom si zachováva poradie, v ktorom bol systém pôvodne zvýšený:

Krok 3: Vypočítajte i₁

Jo₁ = Δ₁/Δ = 300/1900 = 0.16 a

Krok 4: Vypočítajte δ₂

 Krok 5: Vypočítajte i₂

Jo₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Príklad 2

Určite prúd a napätie prostredníctvom každého odporu v nasledujúcom obvode pomocou metódy sieťových prúdov:

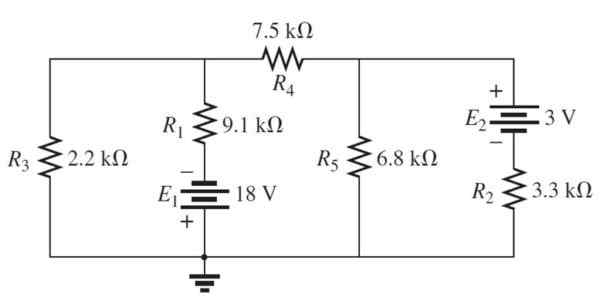Obrázok 4. 3 okruh siete. Zdroj: Boylestad, r. 2011. Úvod do analýzy obvodu.Druhý. Vydanie. Pearson.

Riešenie

V nasledujúcom obrázku sú nakreslené tri sieťové prúdy. Teraz oká bežia odkiaľkoľvek:

Môže vám slúžiť: IMANTÁCIA: Čo pozostáva, metóda a príklady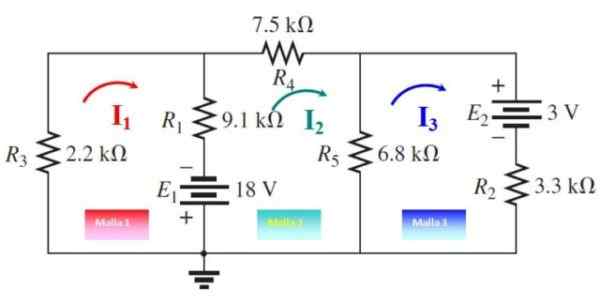 Obrázok 5. Sieťové prúdy pre cvičenie 2. Zdroj: f. Zapata, upravené z Boylestad.

Sieť

-9100.Jo₁+18-2200.Jo₁+9100.Jo₂= 0

-11300 i₁ + 9100.Jo₂ = -18

Sieť       

-(7500 +6800 +9100) .Jo₂ + 9100.Jo₁+6800.Jo₃-18 = 0

9100.Jo₁ - 23400.Jo₂ + 6800.Jo₃ = 18

Mesh 3  

-(6800 + 3300) i₃ + 6800.Jo₂ - 3 = 0

6800.Jo₂ - 10100.Jo₃ = 3

Systém rovníc

-11300 i₁ + 9100.Jo₂ + 0.Jo₃= -18

9100.Jo₁ - 23400.Jo₂ + 6800.Jo₃ = 18

0.Jo₁ + 6800.Jo₂ - 10100.Jo₃ = 3

Aj keď sú čísla veľké, rýchlo sa vyrieši pomocou vedeckej kalkulačky. Pamätajte, že rovnice sa musia objednať a pridať nuly do miest, kde sa neznámy neobjaví, ako sa objavuje tu.

Prúdy sieťoviny sú:

Jo₁ = 0.0012 A; Jo₂ = -0.00048 a; Jo₃ = -0.00062 a

Prúdy Jo₂ a Jo₃ Cirkulujú v opačnom smere na obrázku, pretože sa ukázalo, že sú negatívne.

Tabuľka prúdov a napätia v každom odporu

Odpor (Ω)	Prúd (AMPS)	Napätie = i.R (volty)
9100	Jo1 -Jo2 = 0.0012-(-0.00048) = 0.00168	pätnásť.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	Jo2 -Jo3= -0.00048-(-0.00062) = 0.00014	0.95

Riešenie pravidiel Cramer

Keďže sú veľké množstvo, je vhodné použiť vedecký zápis na priamu spoluprácu s nimi priamo.

Výpočet i₁

Farebné šípky v determinante 3 x 3 označujú, ako nájsť numerické hodnoty, vynásobenie uvedených hodnôt. Začnime získaním tých prvej zátvorky v determinant δ:

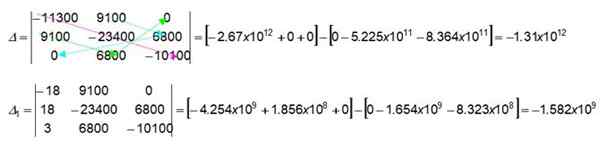
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Okamžite získame druhú konzolu v tom istom determinante, ktorý funguje zľava doprava (pre túto konzolu neboli farebné šípky nakreslené na obrázku). Pozývame čitateľa, aby ho overil:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^jedenásť

6800 x 6800 x (-11300) = -5.225 x 10^jedenásť

Rovnakým spôsobom môže čitateľ overiť aj hodnoty pre determinant Δ₁.

Dôležité: Medzi oboma zátvorkami je vždy negatívny znak.

Nakoniec sa získa prúd Jo₁ cez Jo₁ = Δ₁ / Δ

Jo₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

Výpočet i₂

Postup sa môže opakovať na výpočet Jo₂, V tomto prípade na výpočet determinantu δ₂ Druhý stĺpec determinantu A je nahradený stĺpcom nezávislých výrazov a jeho hodnota sa nachádza podľa vysvetleného postupu.

Avšak, ako je ťažkopádny z dôvodu veľkého počtu, najmä ak neexistuje vedecká kalkulačka, najjednoduchšie je nahradiť hodnotu Jo₁ už vypočítané v nasledujúcej rovnici a jasné:

-11300 i₁ + 9100.Jo₂ + 0.Jo₃= -18 → 9100 i₂= -18 + 11300 i₁ → i₂ = -0.00048 a

Výpočet

Raz s hodnotami Jo₁ a Jo₂ V ruke Jo₃ Priamo sa nachádza nahradením.

Odkazy

1. Alexander, C. 2006. Základy elektrických obvodov. Tretí. Vydanie. MC Graw Hill.
2. Boylestad, r. 2011. Úvod do analýzy obvodu.Druhý. Vydanie. Pearson.
3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 5. Elektrická interakcia. Editoval Douglas Figueroa (USB).
4. Garcia, L. 2014. Elektromagnetizmus. Druhý. Vydanie. Priemyselná univerzita v Santander.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 2.