Charakteristiky amplitúdy vlny, vzorce a cvičenie

Ten Amplitúda Je to maximálny posun, ktorý sa vyskytuje bodom vo vlne vzhľadom na rovnovážnu polohu. Vlny sa prejavujú všade a mnoho spôsobov vo svete okolo nás: v oceáne, vo zvuku a v lane nástrojov, ktorý ho vytvára vo svetle, na zemskom povrchu a oveľa viac.

Jedným zo spôsobov, ako produkovať vlny a študovať jeho správanie, je pozorovanie vibrácií lana, ktoré má pevný koniec. Tým, že sa narušenie na druhom konci, každá častica lana osciluje a s ňou sa energia narušenia prenáša vo forme sukcesie pulzov po celom.

Vlny sa prejavujú mnohými spôsobmi v prírode. Zdroj: Pixabay.

Keď sa energia šíri, lano, ktoré má byť dokonale elastické, prijíma typickú sínusoidálnu formu s hrebene a údoliami zobrazenými na obrázku, ktoré sa nachádzajú nižšie v nasledujúcej časti.

[TOC]

Charakteristiky a význam amplitúdy vlny

Amplitúda A je vzdialenosť medzi hrebeňom a referenčnou osou alebo úrovňou 0. Ak sa uprednostňuje, medzi údolím a referenčnou osou. Ak je narušenie lana mierne, amplitúda A je malá. Ak je narušenie intenzívne, amplitúda bude väčšia.

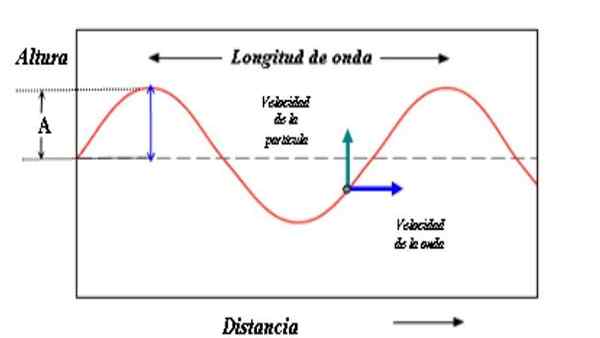Model na opis vlny pozostáva z sínusovej krivky. Amplitúda vlny je vzdialenosť medzi hrebeňom alebo údolím a referenčnou osou. Zdroj: Paco [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Hodnota amplitúdy je tiež miera energie, ktorá nosí vlnu. Je intuitívne, že veľká amplitúda je spojená s väčšími energiami.

V skutočnosti je energia úmerná štvorcovi amplitúdy, ktorá matematicky vyjadrila:

I ∝a²

Môže vám slúžiť: vzájomná indukčnosť: vzorec/koeficient, aplikácie, cvičenia

Kde ja je intenzita vlny, zase súvisiace s energiou.

Typ vlny vyrobenej v príklade lana patrí do kategórie mechanických vĺn. Dôležitým znakom je, že každá častica na lane zostáva vždy veľmi blízko k rovnovážnej polohe.

Častice sa nepohybujú ani nepohybujú lanom. Sa pohybujú hore a dole. Toto je indikované v hornej schéme so zelenou šípkou, avšak vlna spolu s energiou cestuje zľava doprava (modrá šípka).

Vlny, ktoré sa šíria vo vode. Pozorovanie pohybu plachty, ktorý spadol do rybníka, je zrejmé, že jednoducho osciluje sprevádzanie pohybu vody. Nejde príliš ďaleko, aspoň je jasné, že existujú ďalšie sily, ktoré poskytujú iné pohyby.

Vlnový model znázornený na obrázku pozostáva z opakovaného vzoru, v ktorom je vzdialenosť medzi dvoma hrebeňmi vlnová dĺžka λ. Ak chcete, vlnová dĺžka tiež oddeľuje dva rovnaké body od vlny, aj keď nie sú na hrebeňoch.

Matematický opis vlny

Vlnu prirodzene možno opísať matematickou funkciou. Pravidelné funkcie ako sínus a kosínus sú ideálne pre túto úlohu, či chcete reprezentovať vlnu vo vesmíre aj v čase.

Ak nazývame vertikálnu os na obrázku a horizontálnej osi, nazývame ju „T“, potom sa správanie vlny v priebehu času vyjadruje:

y = a cos (Ωt + δ)

Pre tento ideálny pohyb sa každá častice lana osciluje jednoduchým harmonickým pohybom, ktorý vzniká vďaka sile, ktorá je priamo úmerná posunutiu častíc.

Môže vám slúžiť: Dirac Jordan Atomic Model: Charakteristiky a postuláty

V navrhovanej rovnici sú a, co a δ parametre, ktoré opisujú pohyb, ktoré sú k amplitúda predtým definované ako maximálny posun, ktorý sa vyskytuje časticou vzhľadom na referenčnú os.

Argument o kosíne sa volá Fáza pohybu A δ je fázová konštanta, Aká je fáza, keď t = 0. Funkcia kosínus aj sínusová funkcia sú vhodné na opísanie vlny, pretože sa líšia iba jeden od druhého π/2.

Zvyčajne je možné zvoliť t = 0 s δ = 0 na zjednodušenie výrazu, získanie:

y = cos (Ωt)

Keď sa pohyb opakuje v priestore aj v čase, existuje charakteristický čas, ktorý je obdobie t, definovaný ako čas potrebný na vykonanie úplnej oscilácie častíc.

Popis vlny v čase: charakteristické parametre

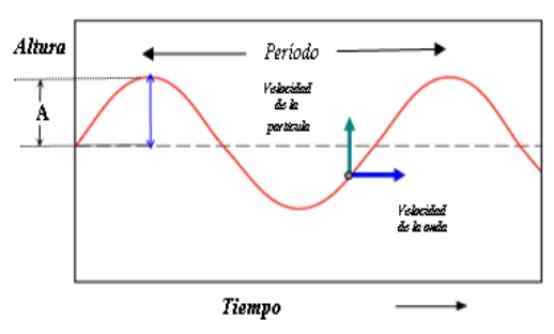Tento obrázok ukazuje opis vlny v čase. Vzdialenosť medzi hrebeňmi (alebo údoliami) teraz zodpovedá obdobiu vlny. Zdroj: Paco [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Teraz, prsník aj kosínus zopakujú svoju hodnotu, keď sa fáza zvyšuje v hodnote 2π, takže:

Ωt = 2π → Ω = 2π /t

Ω sa volá uhlová frekvencia pohybu A má rozmery inverzie času, keďže sú jej jednotkami v medzinárodnom systéme Radián / druhý alebo druhý^-1.

Konečne môžete definovať Frekvencia pohybu F, ako inverzná alebo recipročná doba. Predstavuje počet hrebeňov za jednotku času, v takom prípade:

F = 1/t

Ω = 2πf

F a co majú rovnaké rozmery a jednotky. Okrem druhého^-1, čo sa nazýva Hertz alebo Hertzio, je bežné o tom počuť Revolúcie za sekundu ani revolúcie za minútu.

Vlnová rýchlosť vložka, ktoré je potrebné zdôrazniť, že to nie je to isté ako tie, ktoré zažívajú častice, sa dá ľahko vypočítať, ak sú známe vlnová dĺžka λ a frekvencia f:

Môže vám slúžiť: svetelné telá: Charakteristiky a spôsob, akým generujú svoje vlastné svetlo

V = λf

Ak oscilácia, ktoré sa vyskytujú časticami, je jednoduchým harmonickým typom, uhlová frekvencia a frekvencia závisia iba od povahy oscilujúcich častíc a charakteristík systému. Amplitúda vlny neovplyvňuje tieto parametre.

Napríklad pri hraní hudobnej poznámky na gitare bude mať poznámka vždy rovnaký tón, hoci sa dotýka väčšia alebo menšia intenzita, týmto spôsobom bude vždy znieť ako DO, hoci je počuť silnejšie alebo mäkšie kompozícia, buď na klavíri alebo na gitare.

V prírode sú vlny, ktoré sa prepravujú v materiálnom prostredí vo všetkých smeroch. Z tohto dôvodu sa amplitúda znižuje s inverziou vzdialenosti r na zdroj, ktorý je možné potvrdiť:

A∝1/R

Cvičenie

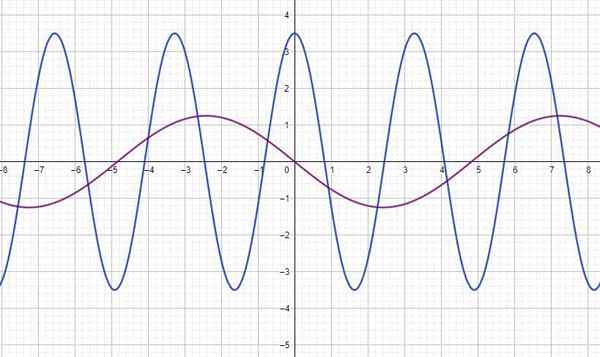
Obrázok zobrazuje funkciu y (t) pre dve vlny, kde a je v metroch a tón v sekundách. Pre každú z nich nájdete:

a) amplitúda

b) Obdobie

c) frekvencia

d) rovnica každej vlny z hľadiska prsníkov alebo cosenos.

Odpovedať

a) Meria sa priamo z grafu pomocou mriežky: Blue Wave: A = 3.5m; Fuchsia Wave: A = 1.25 m

b) Tiež číta graf, určujúci oddelenie medzi dvoma vrcholmi alebo dolinami, po sebe nasledujúce: modrá vlna: t = 3.3 sekundy; Fuchsia Wave t = 9.7 sekúnd

c) Vypočítava sa, že si pamätá, že frekvencia je recipročná doba: modrá vlna: f = 0.302 Hz; Fuchsia Wave: F = 0.103 Hz.

d) modrá vlna: y (t) = 3.5 cos (Ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia Wave: y (t) = 1.25 hriech (0.65T) = 1.25 cos (0.65T+1.57)

Všimnite si, že vlna Fuchsia je zastaraná π/2 vzhľadom na modrú, čo je možné reprezentovať ju so sínusovou funkciou. Alebo posunuté kosínus π/2.